Si intende un approccio strutturato al cambiamento negli individui, nei gruppi, nelle organizzazioni e nelle società che rende possibile (e/o pilota) la transizione da un assetto corrente ad un futuro assetto desiderato.
La parola cambiamento è spesso usata come sinonimo di transizione ma possiede un significato più generico, mentre la parola transizione proviene da un contesto più scientifico. In genetica per esempio la transizione è un tipo di mutazione mentre in fisica indica il passaggio di un sistema da uno stato ad un altro in politichese ???; entrambi questi contesti attribuiscono alla parola transizione un significato più preciso che richiama in modo appropriato la dinamica insita nel concetto di cambiare.
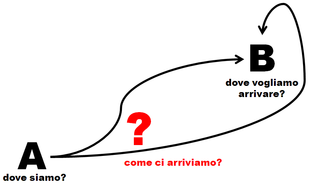
Quando si parla di transizione si è più facilmente consapevoli della sfida connaturata alla necessità e/o alla volontà di trasformare una situazione esistente in una nuova e si è più consapevoli dell’importanza di definire lo stato della situazione corrente [dove siamo?], quello della situazione desiderata [dove vogliamo arrivare?] e il percorso più conveniente [come ci arriviamo?]. Perciò nell’utilizzo che se ne farà il termine transizione esprimerà una connotazione più attiva (che esprime maggiormente il punto di vista di chi la transizione la desidera e/o la guida), mentre il termine cambiamento esprimerà una connotazione più passiva (che esprime maggiormente il punto di vista di chi il cambiamento lo subisce).
La continuità è una funzione che, intuitivamente, fa corrispondere elementi arbitrariamente vicini del dominio elementi arbitrariamente vicini del codominio (anche se ci sono casi di funzioni continue “controintuitive”).
Esistono diverse definizioni di continuità, corrispondenti ai contesti in cui vengono utilizzate: la continuità di una funzione è uno dei concetti di base della topologia e dell’analisi matematica.
La continuità di una funzione può essere definita anche in modo locale: in questo caso si parla di continuità in un punto del dominio.
Una funzione che non è continua è detta discontinua, e i punti del dominio in cui non è continua sono detti punti di discontinuità Nel caso di una variabile reale, spesso la continuità è presentata come una proprietà: la funzione è continua se il suo grafico è formato da un’unica curva che non compia mai salti.
Sebbene questa nozione possa essere usata nei casi più semplici per distinguere funzioni continue da funzioni discontinue, non è formalmente corretta, e può portare ad ambiguità o errori.
Una funzione si definisce continua nel punto del suo dominio se il suo limite è tendente a coincide con la valutazione della funzione Una funzione continua è sempre integrabile è sono integrabili tutte le funzioni.
Continuità per successioni
Una funzione a valori reali è continua per successioni, per ogni successione a valori nel dominio della funzione e convergente a, la successione converge a……….
